
You can only assemble your triangle in one way, no matter what you do. Now shuffle the sides around and try to put them together in a different way, to make a different triangle. Cut the other length into two distinctly unequal parts. You can replicate the SSS Postulate using two straight objects – uncooked spaghetti or plastic stirrers work great.Ĭut a tiny bit off one, so it is not quite as long as it started out.
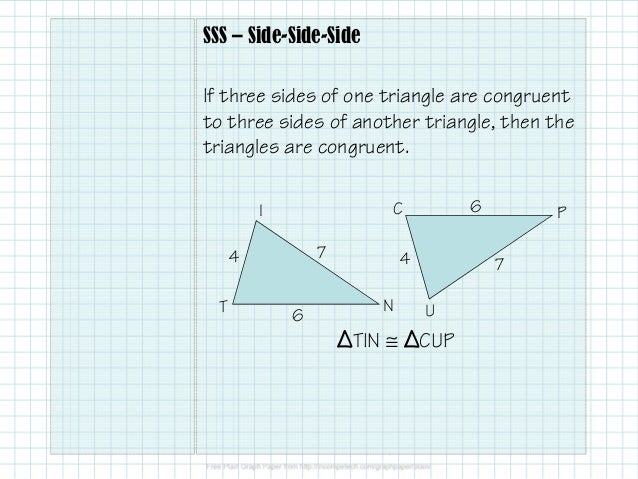
This is the only postulate that does not deal with angles. Perhaps the easiest of the three postulates, Side Side Side Postulate (SSS) says triangles are congruent if three sides of one triangle are congruent to the corresponding sides of the other triangle. Or the two triangles to be congruent, those three parts – a side, included angle, and adjacent side – must be congruent to the same three parts – the corresponding side, angle and side – on the other triangle, △YAK. Move to the next side (in whichever direction you want to move), which will sweep up an included angle. Notice we are not forcing you to pick a particular side, because we know this works no matter where you start. The SAS Postulate says that triangles are congruent if any pair of corresponding sides and their included angle are congruent. Here, instead of picking two angles, we pick a side and its corresponding side on two triangles. SAS theorem (Side-Angle-Side)īy applying the Side Angle Side Postulate (SAS), you can also be sure your two triangles are congruent. You will see that all the angles and all the sides are congruent in the two triangles, no matter which ones you pick to compare.

So go ahead look at either ∠C and ∠T or ∠A and ∠T on △CAT.Ĭompare them to the corresponding angles on △BUG. The postulate says you can pick any two angles and their included side. You may think we rigged this, because we forced you to look at particular angles. You can only make one triangle (or its reflection) with given sides and angles. This is because interior angles of triangles add to 180°.


 0 kommentar(er)
0 kommentar(er)
